Aperiodic
The images below picture aperiodic tilings. Tilings are covering of the plane by non-overlapping shapes belonging to a finite number of isometry classes. Unlike most familiar tilings, aperiodic tilings do not admit any translation as a symmetry, i.e. they never exactly "repeat" in any direction.
Trapezoid and diamond
The trapezoid and diamond tiling consists of two tile types, a trapezoid and a diamond. It also comes with substitution rules describing how to decompose each of these shapes into smaller copies of themselves, as follows:


The diamonds are marked with a point on the bottom left to make their orientation obvious. By alternating the substitution procedure with an appropriate rescaling multiple times, starting with just one shape, one can cover an arbitrary large portion of the plane. Up to some other subtleties, one can show that in the limit of an infinite number of steps, the whole plane is covered, yielding an aperiodic tiling. Here are some pictures of the trapezoid and diamond tiling. To add variety, in some images certain tiles are omitted, or have their borders thickened.
A systematic exploration of all the substitution rules for this family of tilings is carried out in this project.



L-tiling
Sometimes, the procedure sketched for the kite and diamond tiling works out with a single tile isometry type, like with the L-tiling below.




Pinwheel
In other case, there are two isometry types, mirror of each other, this is the case for Conway's famous Pinwheel tiling, shown here, as well as the next two tilings.




Sphinx




Tridrafter





Kite and dart
Penrose tilings can also be constructed through substitution, although a more subtle one in which the smaller tiles are broken across the larger ones, with their pieces nevertheless appropriately matching in the whole tiling. Here is the famous Kite and Dart Penrose tiling (also known as P2).



Penrose 4d
There is another way of constructing the Rhombus (P3) Penrose tiling. It can be constructed by slicing a five-dimensional cubic lattice by a plane, projecting on the plane the lattice vertices and edges that are close enough to the plane. If the plane has irrational slopes, the resulting tiling is aperiodic. The interesting point is that we can generate a lot of other aperiodic tilings by choosing a different dimension and changin the slopes and offsets of the plane. Here are generalised Penrose tilings coming from a four-dimensional lattice, known as the Ammann-Beenker tiling. They display a local four-fold symmetry, instead of the local five-fold symmetry, corresponding to cyclically permuting the axes of the higher dimensional lattice.




Penrose 6d
Here are tilings one can get in a similar way from a six-dimensional lattice. Notice the local 12-fold symmetry.
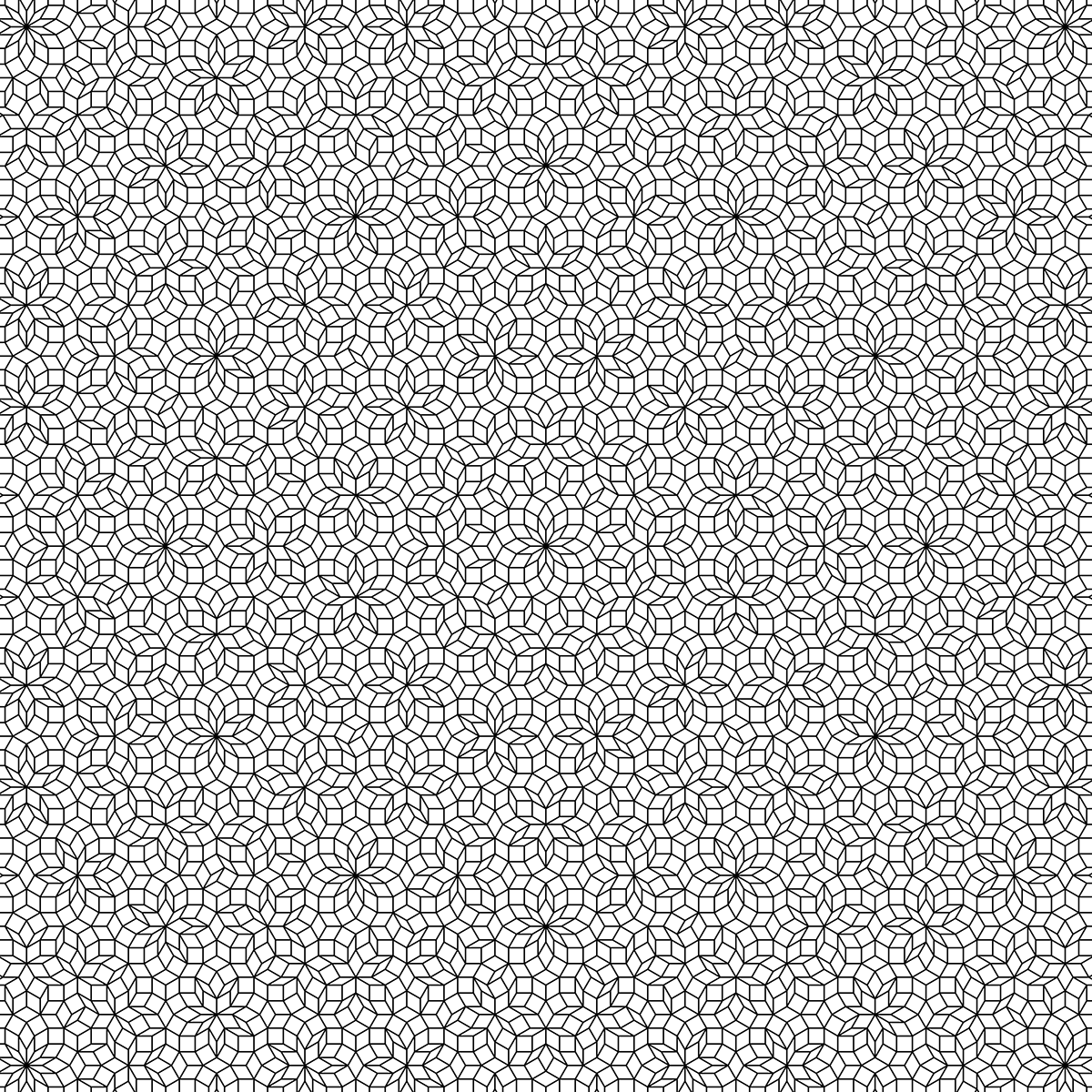



Spiral tilings
Another interesting aperiodic tiling can be obtained by tiling triangles radially. A shift between two half-plane can turn the radial tiling into a spiral one.

























